Game Theory + International Trade = BGR

I think I'm interested in a girl who's a Swiss Korean. She sincerely likes to find out more about me, and she's so pleasant to talk to. She listens and gets excited about topics that I'm excited about, and she shows no lack of self-confidence in expressing and carrying herself. I'm such a sucker for girls who exude lots of self-confidence and show sincerity in trying to know me as a friend. And the best thing is, I can feel that the feeling is mutual. I think I really want to find out more about her.

Now, the only thing is that I have been fully warned about first year relationships. Furthermore, my objective here in the States is to maximize learning and cultural exchange, not to get hitched unecessarily. Therefore, I'm not too sure if I really want to put in efforts into building a Boy-Girl-Relationship (BGR) so early in the semester. I'll do it only if the expected advantages of having a relationship with her outweigh the possible disadvantages.

In order to resolve this dilemma, I did something really geekish, but nonetheless very fun. I applied Game Theory and International Trade. Yeah, you wouldn't believe it but it is so true. I applied John Nash's Equilibrium and David Ricardo's Comparative Advantage Theory to a BGR! Haha. I've got to tell you, it was so much fun. Yeah call me a geek, but check this out first.

According to my objectives, a BGR will bring the following benefits and detriments:

Benefits:

1. Someone to share my life with: I have so much stories to tell, and I love to hear stories from my girl as well. It feels good to share. (Expected possibility: 90%)

2. Cultural Exchange: Different individuals bring with them different abilities and opinions on the same issues. And by trading abilities and ideas, new solutions can be applied to old problems. Sounds familiar? Yes it is! It is nothing but Ricardo's basic model of trade - even though I can be absolutely more productive in everything, from logic to arts, dancing to sports, I will have less comparative advantages in some fields and more in others. Hence, if I specialize in things that I have comparative advantages in, relative to my girl, and my girl does likewise, we can both learn more by exchanging abilities and ideas. (Expected possibility: 100%)

3. Peer Motivation: I'll very much like to know how Koreans motivate themselves to learn. They have such inherent competitiveness in them and I truly admire that. International Trade in action! (Expected possibility: 50%)

Average possibility: 80%

Detriments:
These are selfish concerns, but no less important. If we can't take care of ourselves, how can we take care of others?

1. Monetary Costs: We all know how expensive a relationship can be. No need to elaborate on that. (Expected possibility: 100%)

2. Time Costs: And we also know that each of us face a time constraint (namely 24hours each day if you haven't figured it out), so getting involved in a BGR necessarily means forgoing other activities that will yield me fun and happiness, peace and joy. I'm not over-stretched at this moment, but still, there are things that I'm absolutely comfortable doing by myself. (Expected possibility: 70%, a BGR can be fun too!)

3. Learning Costs: The down side of a BGR is that we might spend too much time sorting out differences that we ought to accept from the start, to the detriment of learning and studying. That is, of course, directly compromising my aim of maximizing learning during my time here in US. This uncannily resembles the negative effects US's trade quotas on its China textile imports have on the two economies. (Expected possibility: 50%)

Average possibility: 73%

So, with the possible payoffs known, we can now proceed to preferences. Assuming that all individuals, including me and the girl that I'm interested in, are rational ie. we place higher values on combinations of things/activities that bring us joy, then we will prefer benefits to detriments. Sounds stupid? Yeah it is. But this is how economics work: it develops elaborate assumptions to spell out simple emotions that we take for granted as highly evolved humans. Well, we think we are, but sometimes when you look back upon history, we have done some really stupid things. So elaborate assumptions that states the facts starkly might not be so bad after all. At least we are clear about what we like and don't.

So, we have a game of two players ie. the girl and I. Let them be Player A and Player C.

Given the expected payoffs, players have two action profiles: Stay Single (s) or Get Attached (a) Of course, getting attached with someone other than each other is still counted as getting attached. We will differentiate the two as: a^c and a^a, if Player A and Player C get together with each other, and a^-c and a^-a, if they have a relationship with someone that yields less expected benefits and more expected detriments than with each other. (This is of course, a huge assumption that falls apart if we find out that the we can both get together with someone better. I'll address this issue later.)

Hence, we get the following preferences, given expected benefits and detriments:

1. Player A prefers getting attached to C than when both are single (benefits outweigh detriments 80% to 73%), which is then preferred to she being single and C getting attached to someone else. This is, in turn, preferred to the case of she getting attached to someone else and C staying single.

ie. A prefers (a^c, a^a) to (s, s) to (s, a^-a) to (a^-c, s)

2. Player C prefers getting attached to A than when both are single, which is then preferred to he being single and A getting attached to someone else. Similarly, this is in turn preferred to the case of he getting attached to someone else and A staying single.

ie. C prefers (a^c, a^a) to (s, s) to (a^-c, s) to (s, a^-a)

Therefore, we have a game like this:

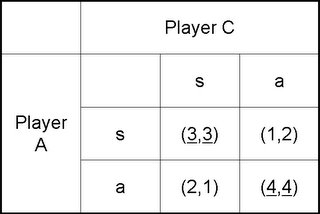
And what do we have here? A Battle of the Sexes game. The underlined numbers are the preferred payoffs of each player given the strategy of the other person. So, if A wants to stay single, I'll prefer staying single to getting attached to somebody else, so I'll stay single. If A doesn't reject my advances, then I'll prefer getting attached to her. Vice-versa.

Thus, we have two corner solutions and we will need a first mover to resolve this game. The first mover, of course, will have the luxury of determining what he wants to do. Given expected payoffs, I'm so going to put in some effort to try to know her.

Now, back to our big assumption that we are the best for one another. This can, of course, not materialize after a few dates. So, we will alter our preferences such that expected payoffs are altered in favour of detriments. Given that we both have to put in alot more efforts to find better girls or guys for ourselves within a few days, the following happens:

A prefers (s, s) to (s, a^-a) to (a^-c, a^-a) to (a^-c, s); and C prefers (s, s) to (a^-c, s) to (a^-c, a^-a) to (s, a^-a)

That gives us the following game:

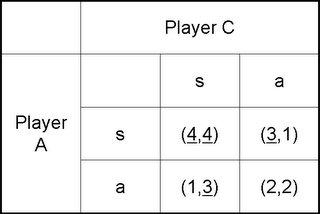Hence, we are both better off staying single.

So you see, BGR with economics, as geekish as it sounds, can be really fun. With continual interactions, first mover will decide if he will stay single or get attached, so he has all the advantage.

So, this is the plan: I'm gonna hang out at her favourite hangout place for an entire week for an hour per night to create chances to know her better. And once we verify the expected benefits and detriments of a relationship with her, we shall decide whether to stay single or to make my moves.